一个人工神经网络(Artificial Neural Network, ANN)其实就是一个计算模型,其灵感来自于人类大脑中生物神经网络处理信息的方式。人工神经网络在机器学习和科研行业引起来不小的热潮,其中已经不乏很多突破性的成果,例如 语音识别、计算机视觉、文字处理、计算机决策等等。在这篇文章中,我们将尝试开发一个流行的人工神经网络—多层感知器。
单一神经元
在神经网络计算中,计算最基本的单元是—神经元(neuron),通常又称为节点(node)或者*单元(unit),它从一些其他节点或从外部源接收输入并计算输出。每个输入都会关联一个权值(weight),它是相对于其他输出的相对重要性而分配的。除了输入层节点外,每个节点为一个计算单元,可以通过一个计算函数f对输入进行加权求和,如下图所示:
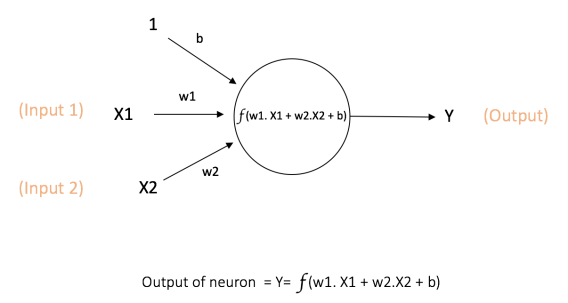
上面的网络从输入X1和X2获取数值,并从节点关联的w1和w2中获取权重。另外还要一个输入1,关联的权重为b(Bias:偏置)**。我们将在后面详细解释偏置。
在上图中计算的结果输出为Y。计算函数f是非线性的,也叫做激活函数。激活函数的目的是将非线性引入到神经元的输出中。这非常重要,因为大多数真实世界的数据是非线性的,我们希望神经元学习这些非线性的描述。
每个激活函数(或者非线性)都采用单个数据并对其执行某个固定的数学运算。 在实践中可能会遇到几个激活函数:
-
Sigmoid: 获取真实值进行输入,并将其压缩到0和1的范围
σ(x) = 1 / (1 + exp(−x)) -
tanh: 获取真实值进行输入,并将其压缩到范围[-1,1]
tanh(x) = 2σ(2x) − 1 -
ReLU: ReLU代表整流线性单元。采用真实值输入且阈值为0(使用0替换负值)
f(x) = max(0, x)
下图展示了三种激活函数:
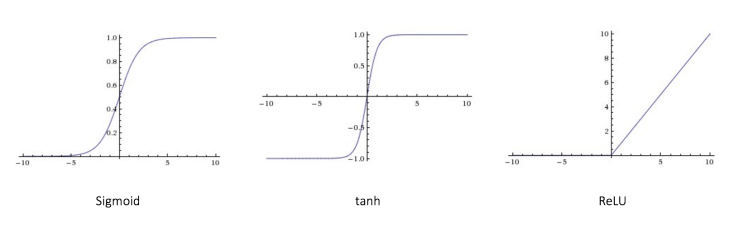
偏置的重要性:Bias的主要功能是为每个节点提供可训练的常数值(除了节点接收的正常值外)。可以参考this link了解更多关于Bias的知识。
前馈神经网络
前馈神经网络是第一个也是最简单的人工神经网络设计。其包含了多层的排列的神经元(节点)。相邻层之间的节点具有连接或者边,所有的这些连接都有权重向关联。
下图是一个前馈神经网络的网络设计:
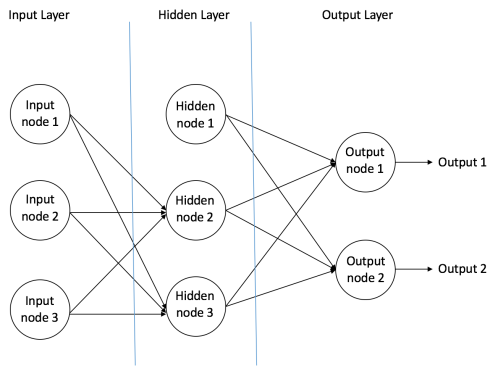
一个前馈神经网络有一下三种类型的节点组成:
- 输入节点 — 输入节点提供了从外界世界到神经网络的信息,统称为“输入层”。在输入层中不进行任何的计算 — 它们只是将信息传递给后面的隐藏节点。
- 隐藏节点 — 隐藏节点没有和外界世界进行直接的连接(因此也叫做“隐藏层”)。它们进行计算,并在输入节点和输出节点之间进行信息传递。隐藏节点的集合叫做“隐藏层”。当一个前馈神经网络只有单一的输入层和单一的输出层,它可以包含多个隐藏层或者没有隐藏层。
- 输出节点 — 输出节点统称为“输出层”,并负责计算和将信息从网络传输到外部世界。
在前馈网络中,信息的移动只有一个方向 – 前向 – 从输入层获取信息,通过隐藏层(如果有),最后到达输出层。在网络中没有环或者循环。Feedforward neural network
前馈神经网络的两个示例如下:
- 单层感知器 — 这是最简单的前馈神经网络,并且不包含任何隐藏层,可以在Single-layer Neural Networks (Perceptrons)和Single Layer Perceptrons 学习了解。
- 多层感知器 — 多层感知器包含一个或者多个隐藏层。我们将只讨论下面的多层感知器,因为它们比单层感知器更有用于当今的实际应用。
多层感知器
一个多层感知器(MLP)包含一个或者多个隐藏层(除了一个输入层和一个输出层)。单层感知器可以学习线性函数,多层感知器可以学习非线性函数。
前馈神经网络部分的样图中,就是一个包含单个隐藏层的多层感知器,所有的连接都有相关联的权重,但上图中仅仅显示了(w0,w1,w2)三个而已。
输入层: 输入层含有三个节点,Bias节点有一个值 1,其他两个节点将 X1 和 X2 作为外部输入(取决于输入数据集的数值)。前面已经讲过,在输入层不进行任何的计算,因此输入层的输出分别是 1,X1 和 X2,其被馈送到隐藏层。
隐藏层: 隐藏层同样含有三个节点,其中Bias节点带有一个输出值 1 。隐藏层其他节点的输出取决于和该节点连接(边)的输入层(1,X1,X2)以及其相关联的权重。下图展示了其中一个节点(亮色表示)的输出。同样,其他节点的输出都是被计算过的,还记得之前讲过的激活函数f吗。计算后的结果会馈送给输出层:
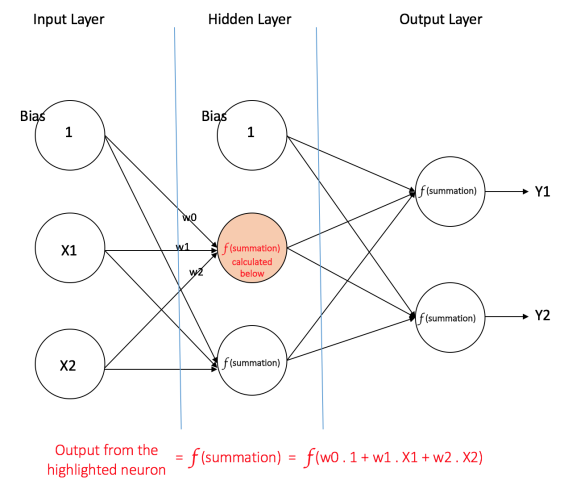
输出层: 输出层有两个节点,它们从隐藏层接收输入,并执行与亮色显示的隐藏节点所示的计算。计算的结果(Y1和Y2)就是这个多层感知器的输出。
给定一组特征X = (x1, x2, …)和目标y,多层感知器可以学习特征和目标之间的关系,以用于分类和回归。
让我们使用一个示例来解释多层感知器,以更好的理解。假设我们有一组关于学生标记的数据集:
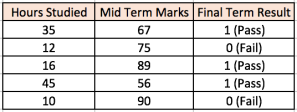
前两个输入栏显示的是学生学习的小时数和学生中期考核。最终的结果列有两个值 0 或者 1 ,表示学生是否通过了期末考核。例如,可以看到,如果学生学习了35个小时,并在中期获得了67分,他/她就最终通过了期末考核。
但是如果有一个新的学生,其学习的时长为25个小时,中期得到70分,其是否通过最后的期末考核呢?

这其实是一个典型的二元分类问题,多层感知器能够从给定的示例(训练数据)中学习并且能够在新的数据点下给出执行的预测。我们将在下面看到多层感知器是如何学习这样的关系的。
训练我们的MLP:反向传播算法
多层感知器学习的算法叫做反向传播算法。我建议阅读这个Quora答案Hemanth Kumar(下面引用),这解释了反向传播明确。
Backward Propagation of Errors, often abbreviated as BackProp is one of the several ways in which an artificial neural network (ANN) can be trained. It is a supervised training scheme, which means, it learns from labeled training data (there is a supervisor, to guide its learning).
To put in simple terms, BackProp is like “learning from mistakes“. The supervisor corrects the ANN whenever it makes mistakes.
An ANN consists of nodes in different layers; input layer, intermediate hidden layer(s) and the output layer. The connections between nodes of adjacent layers have “weights” associated with them. The goal of learning is to assign correct weights for these edges. Given an input vector, these weights determine what the output vector is.
In supervised learning, the training set is labeled. This means, for some given inputs, we know the desired/expected output (label).
BackProp Algorithm: Initially all the edge weights are randomly assigned. For every input in the training dataset, the ANN is activated and its output is observed. This output is compared with the desired output that we already know, and the error is “propagated” back to the previous layer. This error is noted and the weights are “adjusted” accordingly. This process is repeated until the output error is below a predetermined threshold.
Once the above algorithm terminates, we have a “learned” ANN which, we consider is ready to work with “new” inputs. This ANN is said to have learned from several examples (labeled data) and from its mistakes (error propagation).
现在已经对反向传播有了一定的了解,让我们回到上面学生标记的问题中。
设想,我们的多层感知器中包含两个输入节点(除去Bias节点),分别用于“学生学习小时数”和“中期考核成绩”,同样含有一个隐藏层包含两个节点(除去Bias节点),输出层同样含有两个节点 — 上层节点输出“通过”的概率,而下层节点输出“失败”的概率。
通常使用Softmax 函数作为多层感知器输出层中的激活函数,以确保输出是概率,并且相加为 1 。Softmax函数使用任意真实数据的向量,并将其压缩为 0 和 1 之间的值得向量,其总和为 1。因此,在这种情况下:
Probability (Pass) + Probability (Fail) = 1
Step 1: 前向传播
网络中的权重都是随机分配的。让我们考虑下面图中标记为V的隐藏层节点。假设从输入到该节点的连接的权重是w1,w2和w3(如图所示)。
然后网络将第一组训练样本作为输入(我们知道第一组的输入为35何67,通过的概率为1)。
- 输入网络 = [35,67]
- 希望网络(目标)的输出 = [1,0]
然后考虑中的节点的输出 V 能够按照如下的公式计算(f是类似sigmoid的激活函数):
V = f(1*w1 + 35*w2 + 67*w3)
同样的,其他隐藏节点的输出也是计算过的。隐藏层两个节点的输入时输入层两个节点的输出。这使我们能够从输出层中的两个节点计算输出概率。
假设输出层两个节点的输出概率分别为 0.4 和 0.6(由于权重是随机分配的,因此输出也是随机的)。我们可以看到计算的概率(0.4 和 0.6)里最终的期望概率(1 和 0)非常远,因此下图被定义为“不正确的输出”。
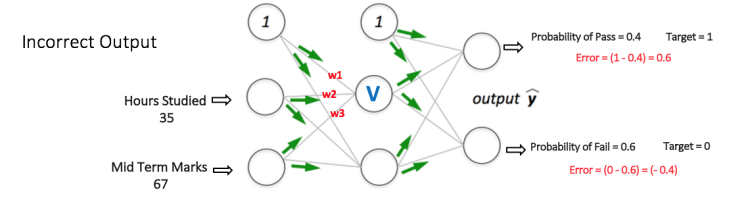
Step 2: 反向传播和权重更新
在上一步中,可以看到计算的输出有很大的误差,我们通过计算输出节点处的总误差,并通过网络使用反向传播将这些误差传播回计算梯度。然后使用一种优化的方法,例如梯度下降来调整所有网络节点中的权重,目的是减小输出层的误差。如下图所示(先忽略下图中的数学方程):
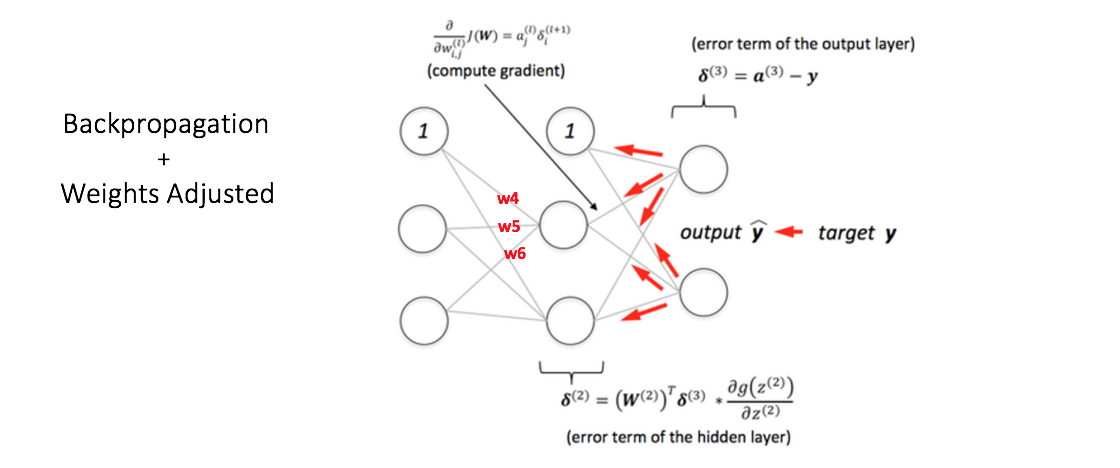
假设与所考虑的节点相关联的新权重是w4,w5和w6(在反向传播和调整权重之后)。
现在,再次使用同样的样本输入到网络中,网络应该比之前更好的执行,因为现在调整了权重以最小化预测中的误差。如下图所示,输出节点的误差已经由之前的[0.6, -0.4]减小到了[0.2, -0.2],这意味着我们的网络已经学会正确的分类第一个训练样本了。
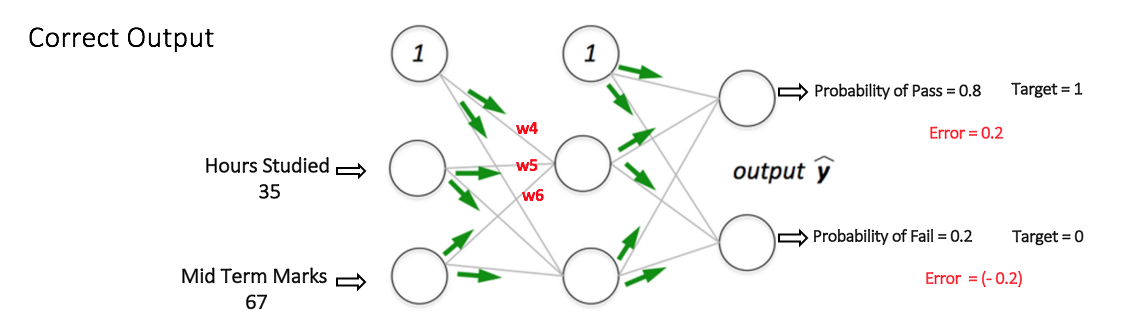
在其他数据集中的训练样本重复这个过程,最后,网络说已经学会了这些样本了。
如果现在需要预测一个学习时长为25小时,中期考核已经得到70分的学生,是否能够在期末考核中通过呢,我们通过正向传播步骤找到最后通过和非通过的概率即可。
在文章中已经忽略了很多的数学方程和概念,例如“梯度下降”等。有关反向传播算法的更多数学参考的讨论,请参阅此链接。
多层感知器的3D可视化
前面虽然讲了那么多多层感知器的理论知识,但是对于学习来说,最好的方式还是能够直观的看到整个感知器的执行过程和结果最好,Adam Harley创建了一个多层感知器的3D可视化工具,并且已经使用反向传播训练了手写数字MINIST的数据集。
网络从一个手写数字的28×28图像(其在输入层中具有对应于像素的784个节点)获取784个数字像素值作为输入。 网络在第一隐藏层中具有300个节点,在第二隐藏层中具有100个节点,在输出层中具有10个节点(对应于10位数字)。
虽然这里描述的网络比我们在前面部分讨论的更大(使用更多的隐藏层和节点),但是正向传播步骤和反向传播步骤中的所有计算都以相同的方式完成(在每个节点) 之前。
下图展示了当输入数字“5”时的网络:
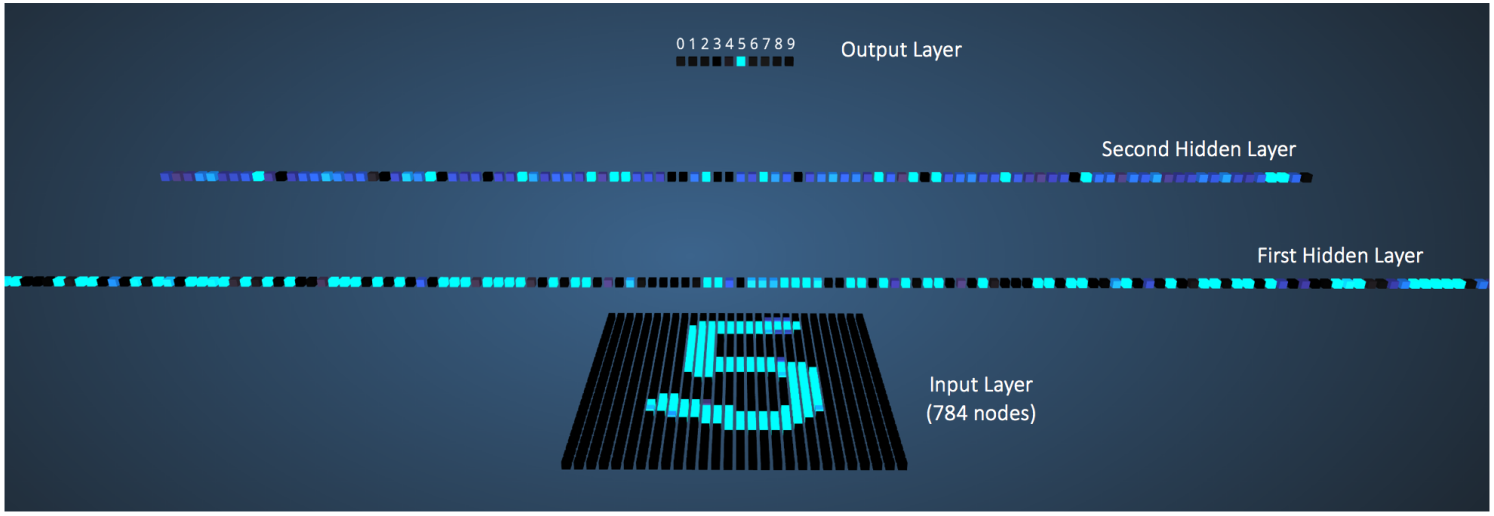
具有比其他输出值更高的输出值的节点由更亮的颜色表示。 在输入层中,亮节点是接收较高数值像素值作为输入的节点。 注意在输出层中,唯一的明亮节点对应于数字5(其输出概率为1,其高于输出概率为0的其他九个节点)。 这表示MLP已正确分类输入数字。
深度神经网络
- What is the difference between deep learning and usual machine learning?
- What is the difference between a neural network and a deep neural network?
- How is deep learning different from multilayer perceptron?
总结
这篇文章到此算是一个结束,文章中还有很多的数学工程和相关概念没有解释,就当做后续继续学习的动力吧。
本文针对神经网络进行了简单的介绍,对其中的多层感知器进行了说明和举例,但是多层感知器的内容不仅限于此,在不断地学习中会有更多内容和新知识会遇到,不断地努力才是正道。
